首页 CRYPTO

# 反馈移位寄存器

在 GF (2) 上的一个 n 级 FSR 通常由 n 个二元存储器和一个反馈函数组成

img

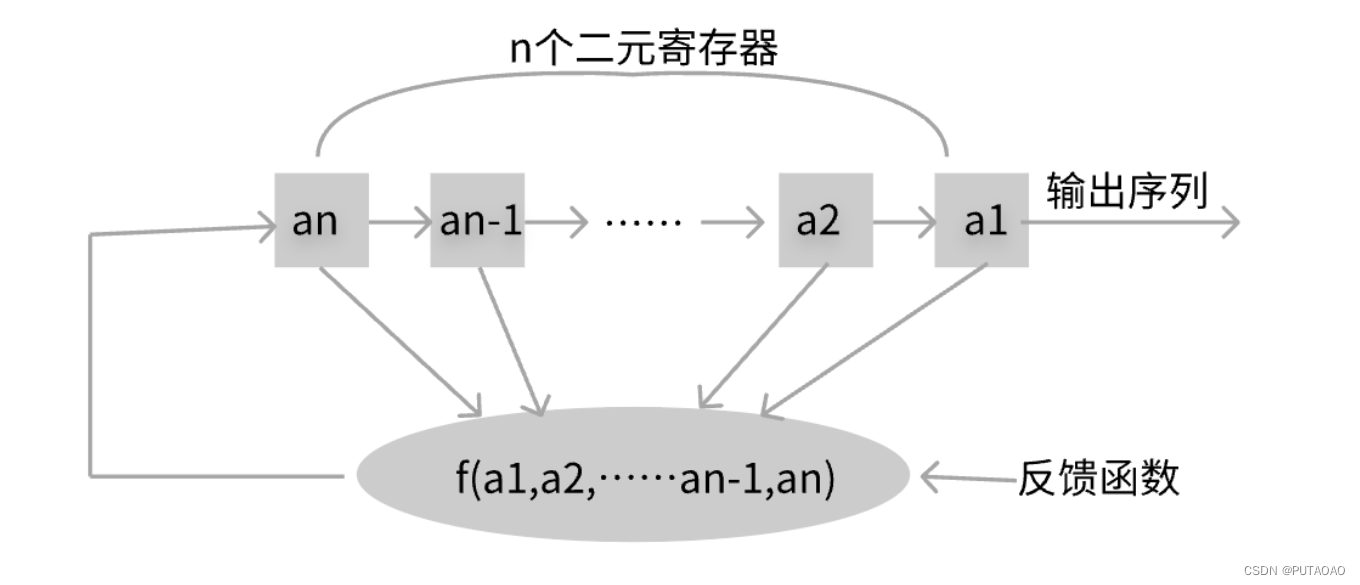
当反馈函数是线性的我们则将其称为 LFSR

反馈函数可表示为

f(a1,a2,……,an−1,an)=cna1⊕cn−1a2⊕……c1anf(a_1,a_2,……,a_{n-1},a_n)=c_na_1⊕c_{n-1}a_2⊕……c_1a_n

# 举个栗子

给定一个 5 级的 LFSR，其初始状态为

(a1,a2,a3,a4,a5)=(1,0,0,1,1)(a_1,a_2,a_3,a_4,a_5)=(1,0,0,1,1)

反馈函数

f(a1,a2,a3,a4,a5)=a4⊕a1f(a_1,a_2,a_3,a_4,a_5)=a_4⊕a_1

过程图

img

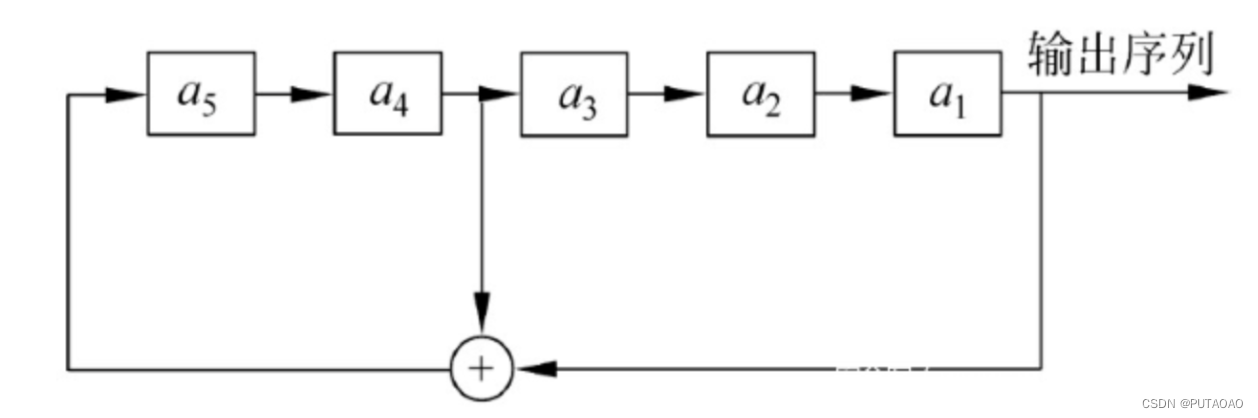
输出序列前 5 位已知 10011

第六位则为

a6=a4⊕a1=0a_6=a_4⊕a_1=0

接下来

a7=a5⊕a2=1a_7=a_5⊕a_2=1

以此推类

对于一个 n 级的 LFSR 来讲，其最大周期为2n−12^n-1，因此对于我们上面的 5 级 LFSR 来讲，其最大周期为25−1=312^5-1=31。

从上面可以看出，LFSR 主要关心三个部分，初始状态，反馈函数和输出序列

一般遇到题目都是已知反馈函数和输出序列，求初始状态

# 题目

# [第七章 CTF 之 CRYPTO 章] LFSR

seed = 0x00000000 # you need to solve this
flag = 'n1book{seed}'
state = seed
mask = 0b10000000000000000000000001010111
def lfsr():
    global state, mask
    output = state & 1
    now = state & mask
    new = 0
    while now:
        new ^= now & 1
        now >>= 1
    state = (new << 31) | (state >> 1)
    return output
for i in range(32):
    lfsr()
print '%x' % state # 155a796b
f=a_1⊕a_2⊕a_3⊕a_5⊕a_7⊕a_
当最后一次 lfsr () 时
new=s_1⊕s_2⊕s_3⊕s_5⊕s_7⊕s_
而s2,s3,s5,s7,s32,news_2,s_3,s_5,s_7,s_{32},new 已知
1658298398172
# exp
state = seed
mask = 0b10000000000000000000000001010111
sts=0x155a796b
key=bin(sts)[2:].zfill(32)
print(key)
mask = '10000000000000000000000001010111'
key='00010101010110100111100101101011'
R = ''
for i in range(32):
    output = key[1:32]+'?'
    out = int(key[0]) ^ int(output[-32]) ^ int(output[-2]) ^ int(output[-3]) ^ int(output[-5]) ^ int(
        output[-7])
    R += str(out)
    key = key[1:32]+ str(out)
print('flag{' + hex(eval('0b' + R)) + '}')
# 2018 CISCN 线上赛 oldstreamgame
flag = "flag{xxxxxxxxxxxxxxxx}"
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==14
def lfsr(R,mask):
    output = (R << 1) & 0xffffffff
    i=(R&mask)&0xffffffff
    lastbit=0
    while i!=0:
        lastbit^=(i&1)
        i=i>>1
    output^=lastbit 
    return (output,lastbit)
R=int(flag[5:-1],16)
mask = 0b10100100000010000000100010010100
f=open("key","w")
for i in range(100):
    tmp=0
    for j in range(8):
        (R,out)=lfsr(R,mask)
        tmp=(tmp << 1)^out
    f.write(chr(tmp))
f.close()
# exp
mask = '10100100000010000000100010010100'
key = '00100000111111011110111011111000'
tmp=key
R = ''
for i in range(32):
    output = '?' + key[:31]
    ans = int(key[-1])^int(output[-3])^int(output[-5])^int(output[-8])^int(output[-12])^int(output[-20])^int(output[-27])^int(output[-30])
    R += str(ans)
    key = str(ans) + key[:31]
R = format(int(R[::-1],2),'x')
flag = "flag{" + R + "}"
print (flag)